A Brief History of Encryption

Posted by Robert on October 29, 2020 · 28 mins read · View Live

As an assignment for one of my MSc modules I had to produce a report on cyber security. I chose to focus on encryption methods. This is the report I produced. It was graded distinction.

1. Introduction

Throughout history there have been necessities for people to send sensitive data, be that battle plans on a road, or their credit card number online. In many instances the users do not want a third party to intercept the data they are sending. This is where encryption comes in.

As it happens, there are records of encryption and concealed secret messages being sent long before the existance of internets and computers. These date as far back as 1900 B.C., when early civilisations would conceal messages pictorially [1], or by use of a scytale. Also used was a class of cipher still discussed today - the Substitution cipher. This report discusses a few of the various uses of encryption throughout history, how the method works, and how it can be broken. In section 2 we discuss prehistoric encryption, which although no longer useful to secure information still provide a good introduction to encryption. This is followed by a discussion of the Enigma device used by the Germans in the 1930’s and 1940’s in section 3. We delve into how it works, and how it was cracked. Finally in section 4 we discuss modern day encryption methods, how they work, and their vulnerabilities.

2. Pre-Historic Networks

Suppose a Roman General wished to invade a city. His regiment is approaching from the north, while another is approaching from the south. Suppose also that he was required to make a last minute change to his battle plan. How should he alert the other regiment of the new plan?. If he sent a messgenger with the now plans how would he ensure that if his messenger was captured the plans wouldn’t fall into enemy hands? He would need a way to encrypt the information such that only he and the other regiment can understand what is written.

While this may seem irrelevant to 21st computer networks and vulnerabilities, it forms one of the earliest examples of encryption (and potentially unwanted decryption). This scenario could also model a simple computer network. The General and his regiments can be modelled as two communicating hosts, his battle plans some sensitive information, and his messenger on the open road, the signal on a wire. As such, it forms a useful starting point for a discussion on encryption.

2.1. The Scytale

The scytale is a cipher often attributed to the Ancient Greeks [2]. It is a cylindrical rod around which paper was wrapped before writing across multiple folds of paper [3].

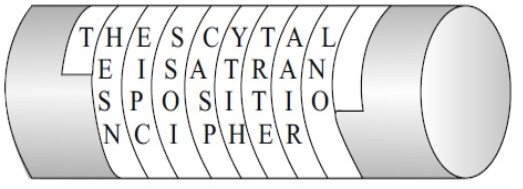Figure 1: A Scytale [4]

This would transpose the message on the paper such that it could only be read if wrapped around a rod of the same diameter.

While easy to encode a message in this way, it is not particularly secure. A third party can see by the nature of the medium used (a long strip of paper) how the message was encoded, and by trial and error decrypt the message.

2.2. Substitution Ciphers

According to Merriam-Webster, a substitution cipher is ‘a cipher in which the letters of the plaintext are systematically replaced by substitute letters’ [5]. These substitute letters are generally referred to as ciphertext. A prominent example of a substitution cipher is the Caesar cipher. This cipher was allegedly used by Julius Caesar to encode sensitive military information [6], hence its name.

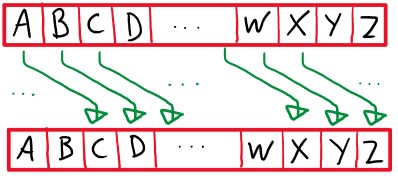Figure 2: A Caesar Cipher with key = 2, based on Figure 1 from Three-Pass Protocol Implementation in Caesar Cipher Classic Cryptography [7]

As shown in figure 2, a Caesar cipher works by shifting each letter k spaces in the alphabet. This produces a mapping which could easily and methodically be applied to the message, the outcome looking like a jumbled string of text. The number of characters by which the message has been shifted is referred to as the ‘key’. Any recipient of the message, could easily reverse the mapping by that number of spaces.

A result of its relative simplicity, is that the Caesar cipher is relatively simple to crack, and certainly isn’t sophisticated enough for modern day needs. As the cipher is cyclical, there are only 25 possible keys. An obvious and simple brute force method would be to attempt a decryption using each key k = 1, k = 2, …k = 25 and select whichever solution seems most realistic given the circumstances. Any moderm computer could crack this quite quickly.

Simple knowledge of the given language, can speed up this significantly, for example if we wished to decode the following ‘K co vjg dguv fwem’, and we know that ‘I’ and ‘a’ are the most likely one letter words in English, we could guess the key is probably +2 or +102 If we guessed +10, and decrypted using −10, we would get ‘A se lzw twkl vmuc’, which is nonsense, however if we decrypted using −2, we would get ‘I am the best duck’. With one assumption, we have decrypted this message in two attempts.

Any data encrypted with this method is relatively easy to crack manually. With a computer, we would be able to crack it in seconds. In section 3, a more complex encryption method (with significant consequences) is discussed.

3. The Enigma and The Bombe

In the Second World War, similar to our Roman exam- ple in section 2, the Germans were required to send

information across long distances, however they didn’t use messengers, they used telegraph. Telegraph is a form of communcation developed in the mid 1800’s by Samuel Morse which relies on sending long and short pulses in morse code [8]. Due to the unencrypted nature of a telegraph signal, its use for transmitting sensitive military information was only viable if there was a way of reliably encrypting the data being sent, and transmitting. As discussed in section 3.1, this is exactly what the Germans did.

3.1. The Working of The Enigma

The Enigma machine was invented in 1919 by Hugo Koch [9], and adopted by the German armed forces to encode all messages before transmitting them. The Germans believed this system to be unbreakable, and that any Enigma-encrypted messages couldn’t be read others.

Figure 3:A labelled photograph of an Enigma machine [10]

The enigma machine has four main parts. The keyboard, lampboard, plugboard, and the rotors (labelled in figure 3). The working of an Enigma is simple. When you press a button on the keyboard, a light on the lampboard for a different letter is illuminated. One would type the message they wished to encode into the keyboard, recording each letter in the process. These encrypted letters could then be transmitted by telegraph.

Despite the device’s foreboding reputation, the inner workings of the Enigma machine is relatively simple. Each time a letter button is pressed, a signal travels through the plugboard (a board where all letters in the alphabet are paired with one other) transforming it to a second letter, through the rotors where it is scrambled to a third letter, back through that letters wire on the plugboard where it is transformed to a fourth letter, which then lights up. To complicate matters further, each time a letter is pressed, the rotors increment one step - if you press a letter multiple times in a row, you would get different outputs each time (for this reason the code couldn’t be broken as in section 2.2) [11]. The recipient could input the coded output into a machine set up the same (and operating in reverse) and they would be able to read the message.

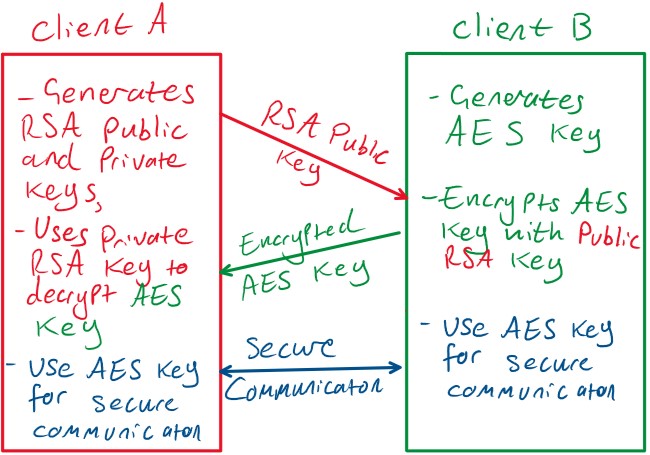Figure 4:A diagram showing how the electrical signal travels in an Enigma machine based on image on Crypto Museum [12]

To crack this code, and read messages being transmitted by the German military, all the Allies needed was to guess the set-up of the machine. However there were a few problems:

  • There were approximately 150∗1012 possible com- binations
  • The Germans changed the setup on a daily basis

Simply guessing the starting position of the enigma was not a reliable method of cracking the code. A systematic approach was needed.

3.2. The Bombe

While impractical to crack manually by brute force, the enigma had 2 significant vulnerabilities which were exploited by British and Polish codebreakers:

  • No letter ever mapped to itself
  • Messages sent by the Germans frequently included standard strings of text, (such as greetings and weather reports)

These two vulnerabilities could be used in tandem to systematically crack the code. By positioning the standard string such that no letter mapped to itself, the codebreakers could take the known string, compared with the intercepted string to find a possible position for the weather report within the ciphertext [13].

Given their initial mapping, they could choose an ansatz for the rotors, and proceed to systematically work through the permeatations of the plugboard and rotors until they have cracked the code. This process is explained very well in the Numberphile YouTube video Flaw in the Enigma Code.

This method would still be impractical to complete every day in time to decrypt all intercepted telegraphs. To break the code on a daily basis, Alan Turing built a machine which used electrical current to simulate each possible setup permeatation of the plugboard and drums which would act as rotors on the enigma [14]. In the internet age, encryption messages such as the Enigma in this section, and the caesar cipher from the previous section are unsuitable to send information securely. Section 4 discusses internet age uses of encryption, and its vulnerabilities and controversies.

4. Internet Age Encryption

So far, we have discussed critical uses of encryption in the past, and the significant effects vulnerabilities have had. This section focuses on modern day uses of encryption on the internet.

4.1. Why Encrypt?

The following two scenarios present examples of how unencrypted data can introduce severe vulnerabilities in systems, leaving systems open to attack.

  • Suppose an online shopper wishes to make a purchase. They input their debit card details into a form, and click pay. Their details are sent across the internet to the shop. Suppose someone was listening, and could read the message being sent from the shopper to the shop. They would then have the customers details, and be able to steal the customers money.
  • Suppose an email account provider stores all their users passwords in plaintext. Suppose an SQL injection attack is carried out revealing all user details on the database. The attacker would then have access to all usernames and passwords in the database. They would be able to log in to any users email address, and access their personal details.

Both of these scenarios could be avoided if the providers had encrypted the data they were using.

4.2. Advanced Encryption Standard

The Advanced Encryption Standard (AES) has been the standard algorithm for encrypting data in the US since 2001 [16]. The AES algorithm uses a 128, 192, or 256 bit key to encrypt 128-bit blocks of text prior to sending them. The AES algorithm is an extremely fast algorithm for a computer to carry out, and would take an average of 100 trillion years to crack by brute force [17].

The AES algorithm works by splitting a 128-bit (16 byte) message into a 4x4 matrix. This undergoes several rounds of substitution and permeatation operations, between which parts of the key are added to the the matrix. The reciever knows the key, and reverses the algorithm on each block of data [18].

While the algorithm is extremely secure, and cannot be cracked by brute force, it has one major flaw. It is symmetric. This means that both the sender and the receiver need to know the same key. For a shopper to encrypt their bank details, they would need a way of getting the key from the online shop. Again, if someone were listening and intercepted the key, they would have access to the data being sent. The customers bank details would no longer be secure. So how can we solve this problem? We need an asymmetric encryption method.

4.3. Rivest-Shamir-Alderman

The Rivest-Shamir-Alderman (RSA) algorithm is one of the oldest and most well-known encryption algorithms. It was released in 1977 by Ron Rivest, Adi Shamir and Leonard Adleman [19]. The advantage of RSA of AES is that RSA is an asymmetric method of encryption. That is, data can be encrypted by one party, and decrypted by the other without them both knowing the key. While this sounds somewhat like magic or telepathy, the algorithm is in fact underpinned by number theory. In a process which will be explained in section 4.3.1, two keys are generated, a public, and a private key. The public key is shared and used to encrypt the data, and the private key is used to decrypt the data. Crucial to RSA is that the encryption process cannot be reversed with the public key - the private key is needed [20].

While RSA has a significant advantage over AES - it is computationally more complex, and thus adds more overheads to a data transfer. It is useful when small amounts of data (such as a credit card number) need transmitting, however for a long sessions it reduces speed. It is however often used together with AES to allow secure encrypted communication [21]. In figure 5, client A generates RSA keys, and sends the public key to client B. Client B generates an AES key, which they encrypt with the RSA public key. This can then be sent to client A securely. Client A can decrypt the message to find the AES key, which is then used throughout the session.

Figure 5:5: A diagram depicting RSA and AES being used to- gether for secure communication, based on informa- tion in RSA vs AES - A Primer [21]

4.2.1. The Algorithm

The RSA algorithm relies on two simple mathematical facts [22]:

  1. Multiplication is easy
  2. Factorisation is hard The algorithm relies on modular arithmetic.

A public and private key are generated from two sufficiently large prime numbers using the following process [24]:

  • Choose large p, q ∈ P
  • Let n = pq
  • Let ϕ(p, q) = (p − 1)(q − 1)
  • Choose e such that e is coprime to ϕ(p, q). e is usually chosen to be 65537, and p and q are usually chosen such that ϕ(p, q) is coprime to 65537
  • Calculate d such that de ≡ 1 (mod ϕ(p, q)), that is the modular inverse of e.
  • The public key is (n, e) and the secret key is d

A numerically encoded message be encrypted using the public key, yet it can only be decrypted using the private key. The following process is used to encrypt, send, and decrypt a message using RSA keys[22]:

  • Assume we have a numerically encoded message m.
  • Assume further we have a public key (n, e).
  • Compute c ≡ me (mod n).
  • Send c, our cyphertext.
  • To decrypt, compute cd ≡ m (mod n) where m is the original message, and d our private key.

The only known method to crack an RSA key is to attempt to factorise our public key, to find d. This is computationally complex. To give an example, in 2010 the record for cracking a 786-bit RSA key (that is, a 232-digit number) was 2 years. They researchers claim the amount of CPU time spent is equivalent to 2,000 years on a standard PC at the time [25]. It is worth noting that the longer the key, the longer the calculation take, but also the longer it takes to crack.

4.4. Hashing

So far in this section we have considered methods of encryption where the encryptor wants a reciever to be able to read the original data. Suppose we return to example 2 in section 4.1. If the company had encrypted their passwords, no attacker could get them. However, if they had used a method we have discussed, and attacker could find the key, they would still be able to decrypt the passwords. Instead, they should use hashing.

Hashing is a one way algorithm is used to convert data into a hashed string. It is not possible to get back to the original data from the hashed string. A hashed password would be stored in the database, and when the user tries to login, their input is hashed by the same algorithm. If it matches the one stored on file they are allowed in [26].

4.4.1. Plain Text Passwords

It may surprise the reader to learn that even some major businesses have neglected to encrypt passwords and users passwords have been leaked as a consequence. Some notable organisations who have fallen foul of this include the IEEE (2011) [27], Yahoo (2012) and Hotmail (2009) [28]. This makes it particularly easy for an attacker to access people personal information should they find access to the database.

4.5. Significant Vulnerabilities

While the methods in this section are strong, they still have vulnerabilities. Suppose an attacker gets hold of the private key, they would be able to decrypt all data being transmitted.

It is expected in the not too distant future a new technology (a quantum computer) would be able to break 2048-bit RSA encryption 8 hours. While this isn’t a threat now, there is a risk that once a computer is capable of breaking RSA in such a short period of time RSA would no longer be a useful form of encryption. Should this be the case, we would need newer and faster algorithms to encrypt our data [29].

Returning to hashing, as discussed in the previous subsection. While it is not possible to reverse the algorithm, there is still a vulnerability. Suppose an attacker got hold of a list of hashed passwords, and knew the algorithm used. They could uncover the passwords by brute force. If the attacker hashed all possible commbinations, and for each output checked the list of hashed strings, whenever they find a match they would know that they have found the password used to generate that hash. By doing this they would be able to slowly crack a list of hashed passwords [30].

5. Conclusion

In this report, we have considerd a selection of key encryption methods, some of which are in use today, and some of which are no longer sufficiently secure.

It is clear that over time, as computers get faster and more advanced, existing encryption methods become easier to crack. However, at a similar rate more layers of complexity can be added to existing methods without increasing computation time, more methods can be strung together, and methods emerge.

It is likely that for the forseeable future the encryption landscape will remain the same, with algorithms being phased out and replaced by newer algorithms, and keys getting longer, as computers get faster. It is likely that the only significant encryption vulnerabilities will arise from poor practice, and failing to encrypt data.

However, there is a concern that if a fully working quantum computer could be developed too soon, keys could be cracked too quickly. It is possible that standard non-quantum computers would be unable encrypt data with sufficiently long keys using the current methods without adding significant time overheads. If this were to happen, it wouldn’t spell an end to secure communication, however it would make the tradeoff between security and efficiency more obvious.

References

  • [1] Icitsuser, “The ancient cryptography history,” Feb 2017. [Online]. Available: http://www.icits2015.net/ancient-cryptography-history/
  • [2] J. M. Norman, “The skytale: An early greek cryptographic device used in warfare: History of information.” [Online]. Available: https://www.historyofinformation.com/detail.php?d=4168
  • [3] [Online]. Available: http://mathcenter.oxford.emory.edu/site/math125/transpositionCiphers/
  • [4] C. Paar and J. Pelzl, Understanding cryptography: a textbook for students and practitioners. Springer, 2011.
  • [5] “Substitution cipher.” [Online]. Available: https://www.merriam-webster.com/dictionary/substitution%20cipher
  • [6] C. Suetonius Tranquillus, A. Thomson, and T. Forester, The Lives of the twelve Caesars. G. Bell and Sons, 1893.
  • [7] B. Oktaviana and A. P. U. Siahaan, “Three-pass protocol implementation in caesar cipher classic cryptography,” IOSR Journal of Computer Engineering, vol. 18, pp. 2278–0661, 07 2016.
  • [8] H. Editors, “Morse code and the telegraph,” Nov 2009. [Online]. Available: https://www.history.com/topics/inventions/telegraph
  • [9] ——, “Enigma key broken,” Nov 2009. [Online]. Available: https://www.history.com/this-day-in-history/enigma-key-broken
  • [10] D. NG, “Enigma machine from world war ii finds unlikely home in beverly hills,” Jan 2015. [Online]. Available: https://www.latimes.com/entertainment/arts/culture/la-et-cm-imitation-game-enigma-machine-david-bohnett-20150122-story.html
  • [11] S. Singh and W. S. Festival, “The enigma machine explained,” May 2013. [Online]. Available:https://youtu.be/ASfAPOiq_eQ
  • [12] Simplified circuit diagram of a 3-wheel Service Enigma. [Online]. Available: cryptomuseum.com/crypto/enigma/working.htm
  • [13] Flaw in the Enigma Code. Numberphile, Jan 2013. [Online]. Available: https://youtu.be/V4V2bpZlqx8
  • [14] T. Sale, The US 6812 Bombe Report 1944 - DECODING GERMAN ENIGMA MACHINE MESSAGES. SIGNAL SECURITY DETACHMENT, 1944. [Online]. Available: https://www.codesandciphers.org.uk/documents/bmbrpt/usbmbrpt.pdf
  • [15] “What is sql injection? tutorial and examples: Web security academy.” [Online]. Available: https://portswigger.net/web-security/sql-injection
  • [16] “Announcing the advanced encryption standard,” Nov 2001. [Online]. Available: http://nvlpubs.nist.gov/nistpubs/FIPS/NIST.FIPS.197.pdf
  • [17] R. Franklin, P. Editor, and T. Security, “Aes vs. rsa encryption: What are the differences?” Jul 2020. [Online]. Available: https://www.precisely.com/blog/data-security/aes-vs-rsa-encryption-differences
  • [18] AES Explained (Advanced Encryption Standard). YouTube, Nov 2019. [Online]. Available: https://www.youtube.com/watch?v=O4xNJsjtN6E
  • [19] “Leonard adleman made rsa encryption history with his invention.” [Online]. Available:https://www.invent.org/inductees/leonard-adleman
  • [20] Sam., “A complete explanation of rsa asymmetric encryption,” Feb 2020. [Online]. Available: https://medium.com/curiositypapers/a-complete-explanation-of-rsa-asymmetric-encryption-742c5971e0f
  • [21] P. Townsend. [Online]. Available: https://info.townsendsecurity.com/rsa-vs-aes-encryption-a-primer
  • [22] “Rsa encryption.” [Online]. Available: https://brilliant.org/wiki/rsa-encryption/
  • [23] “Modular arithmetic,” Oct 2020. [Online]. Available: https://en.wikipedia.org/wiki/Modular_arithmetic
  • [24] G. J. Simmons, “Rsa encryption,” Aug 2012. [Online]. Available: https://www.britannica.com/topic/RSA-encryption
  • [25] T. Kleinjung, K. Aoki, J. Franke, A. Lenstra, E. Thomé, J. Bos, P. Gaudry, A. Kruppa, P. Montgomery, D. A. Osvik, H. te Riele, A. Timofeev, and P. Zimmermann, “Factorization of a 768-bit rsa modulus,” Cryptology ePrint Archive, Report 2010/006, 2010, https://eprint.iacr.org/2010/006.
  • [26] D. Arias, “Hashing passwords: One-way road to security,” Sep 2019. [Online]. Available: https://auth0.com/blog/hashing-passwords-one-way-road-to-security/
  • [27] O. Williams, “Ieee data breach: 100k passwords leak in plain text [update],” Sep 2012. [Online]. Available: https://www.neowin.net/news/ieee-data-breach-100k-passwords-leak-in-plain-text
  • [28] E. Bauman, Y. Lu, and Z. Lin, “Half a century of practice: Who is still storing plaintext passwords?” Ph.D. dissertation, 0AD. [Online]. Available: https://web.cse.ohio-state.edu/ lin.3021/file/ISPEC15.pdf
  • [29] C. Gidney and M. Ekerå, “How to factor 2048 bit rsa integers in 8 hours using 20 million noisy qubits,” 2019.
  • [30] B. Haran, Password Cracking. YouTube, Jul 2016. [Online]. Available: https://www.youtube.com/watch?v=7U-RbOKanYs
  • [31] F. Wenneker, “Wenneker article latex template,” LaTeXTemplates. [Online]. Available: https://www.latextemplates.com/template/wenneker-article
← Previous Project Next Project →